视频：https://www.bilibili.com/video/BV1sA411B73r/?spm_id_from=333.1007.top_right_bar_window_history.content.click&vd_source=484293edcf94a55e368ecf2e0d1fbfce

问题描述：

编辑距离，指的是两个字符串之间，由一个转变成另一个所需的最少单字符编辑操作次数。被允许的转变包括：

• 对于任意一个字符串，在任意位置插入一个字符；
• 对于任意一个字符串，删除任意一个字符；
• 对于任意一个字符串，替换任意一个字符。

例：从sun变到satur需要做3次变换：

1：定义问题

D[i][j]=S1前i个字符变为S2前j个字符的次数，即为距离 S1=sun➡S2=satur ， D[3][5]=3

注意：是改变S1使其变为S2，操作对象为S1

2:问题分解

（1）字符串最后一个字符相等

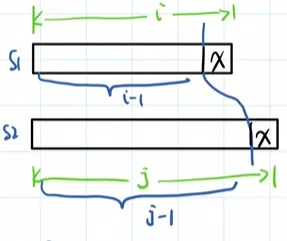
若字符串最后一个字符相等，问题就转变为去掉末尾字符的前一段字符串比较：

即 D[i-1][j-1]。这相当于直接继承左上角单元格的值，操作次数不变

python
展开代码
if S1[i-1]==S2[j-1]：
    D[i][j]=D[i-1][j-1]

（2）字符串最后一个字符不等

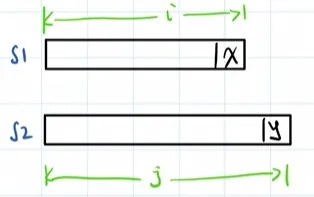
1）插入操作

对S1末尾进行插入操作：

则此操作后，问题变为S1的i个元素和S2的剩下j-1个元素的对比：

D[i][j]=D[i][j-1]+1

+1是操作了一次

2）删除操作

对S1末尾进行删除操作

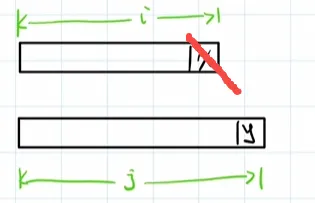
此操作后，问题变为S1的i-1个元素和S2的j个元素的对比：

D[i][j]=D[i-1][j]+1

3）替换操作

对S1末尾进行替换操作

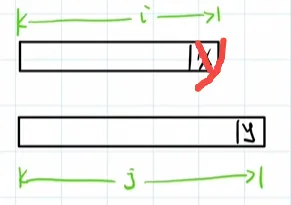
此操作后，问题变为S1的i-1个元素和S2的j-1个元素的对比：

D[i][j]=D[i-1][j-1]+1

要找最少字符变换的最少操作数，就是找：

3：子问题

D[0][0]=0

D[i][0]=i（S1全删了）

D[0][j]=j（S1加j个相同字符）

坐标描述该问题：

• 末尾相同：D[i][j]=D[i-1][j-1]

坐标点移动到左上方

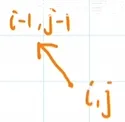
• 插入 D[i][j]=D[i][j-1]+1
• 删除 D[i][j]=D[i-1][j]+1
• 替换 D[i][j]=D[i-1][j-1]+1

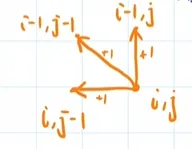
步骤最小者即为D[i][j]下一步的操作：

min{D[i][j-1]+1，D[i-1][j]+1，D[i-1][j-1]+1}

实际例子

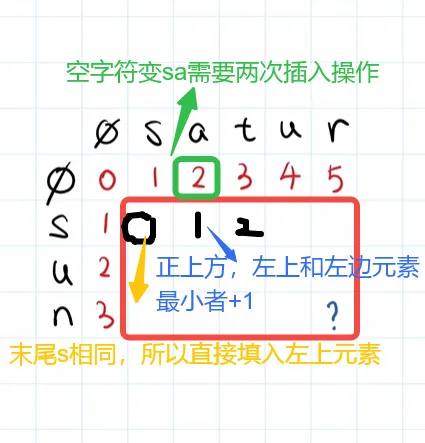
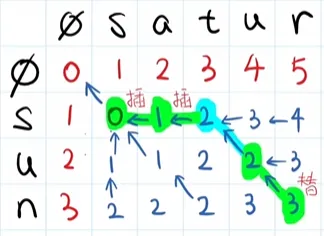
由最终的的图片结果看到D[3][5]=3，所以sun变到satur的最小距离为3

实现代码：

python
展开代码
str1 = input()  # 第一个字符串 s
str2 = input()  # 第二个字符串 t

# 初始化DP表，第0行：[0, 1, 2, ..., len(str2)]
dp = [[x for x in range(len(str2) + 1)] for y in range(len(str1) + 1)]

# 初始化第0列：0, 1, 2, ..., len(str1)
for i in range(1, len(str1) + 1):
    dp[i][0] = dp[i - 1][0] + 1

# 填充DP表
for i in range(1, len(str1) + 1):
    for j in range(1, len(str2) + 1):
        if str1[i - 1] == str2[j - 1]:
            dp[i][j] = dp[i - 1][j - 1]
        else:
            insert_op = dp[i][j - 1] + 1
            delete_op = dp[i - 1][j] + 1
            replace_op = dp[i - 1][j - 1] + 1
            dp[i][j] = min(insert_op, delete_op, replace_op)

print(dp[len(str1)][len(str2)])#输出D[i][j]