cc的记事本
卡尔曼滤波
2026-01-31
控制算法
00

目录

基础公式推导
例子：使用卡尔曼滤波估计某物体真实长度
第一步：计算卡尔曼增益 K_k
第二步：更新状态估计——信息融合的核心步骤
第三步：更新估计误差——代表了对当前新估计的信心度的更新
总结
系统方程
$Q=E\left[\omega \omega^T\right]$的推导过程
如何融合
卡尔曼增益推导过程
卡尔曼滤波数据融合流程
扩展卡尔曼滤波
系统表达
状态方程的泰勒展开
定义状态方程的雅可比矩阵
观测方程的泰勒展开
定义观测方程的雅可比矩阵
扩展卡尔曼滤波的标准更新方程

基础公式推导

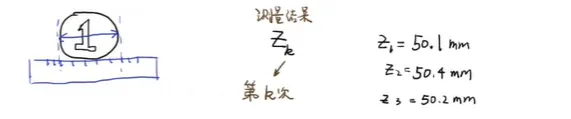
例子：尺寸测量 image.png

测量几次，使用取平均值方法去估计真实数据，其中x^k\hat{x}_k为测量k次的估计值，x^k−1\hat{x}_{k-1}为测量k-1次的估计值

x^k=1k(z1+z2+⋯+zk)=1k(z1+z2+⋯+zk−1)+1kzk=1kk−1k−1(z1+z2+⋯+zk−1)+1kzk=k−1kx^k−1+1kzk=x^k−1−1kx^k−1+1kzk\begin{aligned} \hat{x}_k & =\frac{1}{k}\left(z_1+z_2+\cdots+z_k\right) \\ & =\frac{1}{k}\left(z_1+z_2+\cdots+z_{k-1}\right)+\frac{1}{k} z_k \\ & =\frac{1}{k} \frac{k-1}{k-1}\left(z_1+z_2+\cdots+z_{k-1}\right)+\frac{1}{k} z_k \\ & =\frac{k-1}{k} \hat{x}_{k-1}+\frac{1}{k} z_k \\ & =\hat{x}_{k-1}-\frac{1}{k} \hat{x}_{k-1}+\frac{1}{k} z_k \end{aligned}

即

x^k=x^k−1+1k(zk−x^k−1)\hat{x}_k=\hat{x}_{k-1}+\frac{1}{k}\left(z_k-\hat{x}_{k-1}\right)
  • k↑,1k→0.x^k→x^k−1k \uparrow, \frac{1}{k} \rightarrow 0 . \hat{x}_k \rightarrow \hat{x}_{k-1}

随着k增加，测量结果不再重要

直观理解是有了大量的数据后，对估计结果比较有信心，因此以后的测量值相对而言也就没那么重要了

  • k 小，1k 大，测量值zk 作用较大 k \text { 小，} \frac{1}{k} \text { 大，}\text {测量值} z_k \text { 作用较大 }

测量值和估计值差距较大时，zkz_k作用会被放大

令1k=Kk \frac{1}{k} = K_k，则有

x^k=x^k−1+Kk(zk−x^k−1)\hat{x}_k=\hat{x}_{k-1}+K_k\left(z_k-\hat{x}_{k-1}\right)
 当前的估计值 = 上一次的估计值 + 系数 × (当前测量值 − 上一次的估计值) \text { 当前的估计值 }=\text { 上一次的估计值 }+ \text { 系数 × (当前测量值 }- \text { 上一次的估计值) }

其中KkK_k为卡尔曼增益

公式体现了一种递归的思想，也体现了卡尔曼滤波的优势——不需要追踪很久以前的数据，只需要上一次的就可以了

引入估计误差eESTe_{EST}和测量误差eMEAe_{MEA}，那么卡尔曼增益可以表示为

Kk=eESTk−1eESTk−1+eMGAkK_k=\frac{e_{E S T_{k-1}}}{e_{E S T_{k-1}}+e_{M G A_k}}

在k时刻，若k-1时刻的估计误差远大于k时刻的测量误差，对于x^k\hat{x}_k的取值，认为更加可以信任测量值

eESTk−1≫eMEAk:kk→1x^k=x^k−1+zk−x^k−1=zke_{E S T_{k-1}} \gg e_{M E A_k}: k_k \rightarrow 1 \quad \hat{x}_k=\hat{x}_{k-1}+z_k-\hat{x}_{k-1}=z_k

相反，若测量误差很大时，选择相信上一次的估计值

eESTk−1≪eMEAkKk→0x^k=x^k−1e_{E S T_{k-1}} \ll e_{M E A_k} \quad K_k \rightarrow 0 \quad \hat{x}_k=\hat{x}_{k-1}

例子：使用卡尔曼滤波估计某物体真实长度

在存在测量噪声的情况下，卡尔曼滤波如何最优地估计真实值 image.png 问题设定

  • 真实状态：物体的真实长度 x = 50 mm(一个固定但未知的值，我们试图去估计它)。
  • 初始猜测：我们从一次不准确的推测开始，x̂₀ = 40 mm，并且对这个猜测非常不确定，初始估计误差 e_EST₀ = 5 mm。
  • 测量工具：我们有一个测量仪器，每次测量会带来噪声。从表格看，测量值 Z_k围绕50上下波动 (如51, 48, 47...)，且仪器的测量噪声 e_MEA = 3 mm(恒定)

核心矛盾：我们既有“不准确但动态更新的预测（估计）”，又有“有噪声但反映部分真实情况的观测（测量）”。应该相信哪一个？相信多少？卡尔曼滤波给出了最优的融合方案

卡尔曼滤波的解决方法：三步循环

第一步：计算卡尔曼增益 K_k

Kk=eESTk−1eESTk−1+eMEAK_k=\frac{e_{E S T_{k-1}}}{e_{E S T_{k-1}}+e_{M E A}}

卡尔曼增益是一个 “信任权重”，范围在0到1之间。

它如何解决问题？

  • 分子e_EST：代表我们当前估计的不确定性。这个值越大，说明我们对自己的上一次估计越没信心。
  • 分母加入了 e_MEA：代表测量的不确定性。
  • 逻辑：如果我们自己的估计很不确定(e_EST很大)，而测量相对可靠(e_MEA较小)，那么 K_k就接近1，意味着我们会更相信新的测量值。反之，如果我们自己的估计已经很确定(e_EST很小)，而测量噪声很大，那么 K_k就接近0，意味着我们会更倾向于维持原来的估计。
  • 在例子中：
    • k=1时：K₁ = 5 / (5+3) = 0.625。初始估计误差(5)比测量误差(3)大，所以我们更信任测量，增益值较高。
    • k=2时：K₂ = 1.875 / (1.875+3) ≈ 0.385。经过第一次融合，估计误差变小了(1.875)，我们对估计的信心增加了，因此对新测量的信任权重就降低了。

第二步：更新状态估计——信息融合的核心步骤

x^k=x^k−1+Kk(Zk−x^k−1)\hat{x}_k=\hat{x}_{k-1}+K_k\left(Z_k-\hat{x}_{k-1}\right)

它如何解决问题？

  • (Z_k - \hat{x}_{k-1})是 “测量残差”或“新息”，即测量值与我们上一轮估计的差异。
  • 我们不是简单地用测量值替换旧估计，也不是无视测量值，而是用卡尔曼增益 K_k作为比例，将这个差异的一部分“吸收”到我们的新估计中。
  • 结果：新估计 x̂_k是旧估计和测量值的一个加权平均。K_k决定了向测量值“滑动”多少。
  • 在例子中：
    • k=1：x̂₁ = 40 + 0.625 * (51 - 40) = 46.875。初始估计40和首次测量51的差异是11，我们取了这个差异的62.5%，将估计值从40大幅更新到46.875。
    • k=2：x̂₂ = 46.875 + 0.385 * (48 - 46.875) ≈ 47.308。差异很小(1.125)，且我们只信任了38.5%，所以更新幅度很小。估计值开始收敛。

第三步：更新估计误差——代表了对当前新估计的信心度的更新

eESTk=(1−Kk)eESTk−1e_{E S T_k}=\left(1-K_k\right) e_{E S T_{k-1}}

它如何解决问题？

  • 经过一次融合，我们结合了新的信息，理论上应该对我们得出的新估计更有把握了。
  • 公式 (1 - K_k)必然小于1，所以 e_EST会随着迭代不断减小。这反映了卡尔曼滤波的“学习”过程：随着数据积累，估计的不确定性降低，估计值趋于稳定。

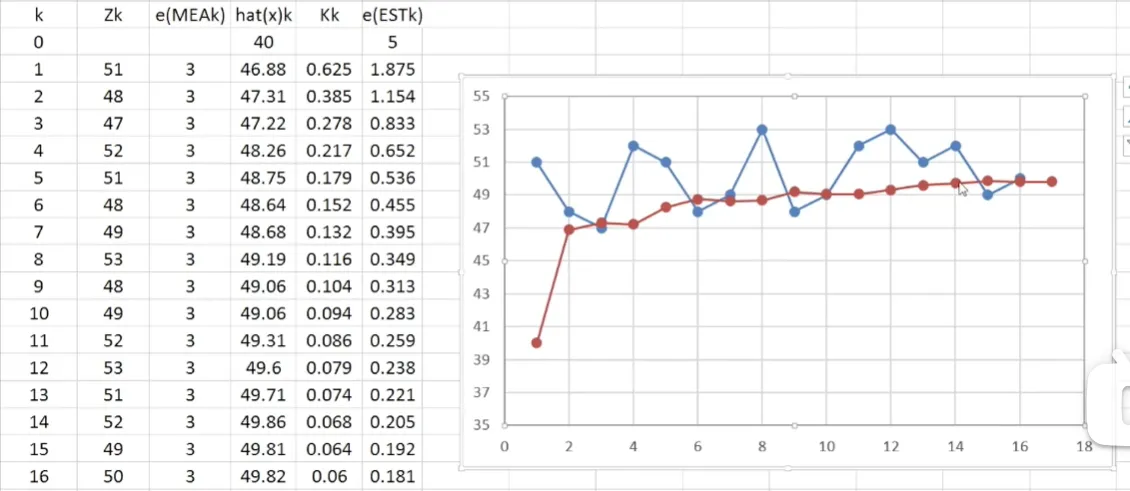
image.png

  • 在例子和Excel表格中：
    • k=1：e_EST₁ = (1-0.625) * 5 = 1.875
    • k=2：e_EST₂ ≈ (1-0.385) * 1.875 ≈ 1.154
    • 从Excel表可以看到，e_EST从5逐渐减小到0.181 (k=16)，估计的置信度越来越高

总结

卡尔曼滤波作用

  • 量化不确定性：始终用数值 (e_EST, e_MEA) 跟踪“预测”和“观测”的可信度。
  • 动态计算权重：通过卡尔曼增益 K，根据双方的可信度实时决定该相信谁多一些。
  • 最优融合：以加权平均的方式，将预测和观测结合起来，得到比单一信息源都更优的新估计。
  • 持续进化：每得到一次新数据，就重复一次“预测→测量→加权融合→更新信心”的循环，使估计值不断逼近真实状态，同时信心不断增强。

因此，卡尔曼滤波解决的就是如何在噪声中通过连续、不确定的观测，智能地估计出一个动态（或静态）系统的最优状态的问题。

系统方程

离散系统的状态空间方程：

Xk=AXk−1+BUkZk=HXk\begin{aligned} & X_k=A X_{k-1}+B U_k \\ & Z_k=H X_k \end{aligned}

往模型中加入不确定性：

  • 模型不准确，加入过程噪声ωk−1\omega_{k-1}
Xk=AXk−1+BUk+ωk−1X_k=A X_{k-1}+B U_k+\omega_{k-1}
  • 传感器不精确，加入测量噪声vkv_k，表示测量过程中产生的不确定性
Zk=HXk+vkZ_k=H X_k+v_k

问题出现：在模型不够准确，测量也不够精确的情况下，如何去估计x^k\hat{x}_k

Q=E[ωωT]Q=E\left[\omega \omega^T\right]的推导过程

过程噪声ωk\omega_{k}满足正态分布P(ω)∼(0,Q)P\left(\omega\right) \sim({0}, Q)

定义"随机噪声"就是均值为0的随机过程，均值不为0的部分称为"偏置"或"系统误差"，不叫"噪声"

  • 噪声向量 ω=[w1w2]\omega=\left[\begin{array}{l} w_1 \\ w_2 \end{array}\right]
  • 转置 ωT=[w1w2]\omega^T=\left[\begin{array}{ll} w_1 & w_2 \end{array}\right]
ωωT=[w1w2][w1w2]=[w1×w2w1×w2w2×w1w2×w2]=[w12w1w2w2w1w22]\omega \omega^T=\left[\begin{array}{l} w_1 \\ w_2 \end{array}\right]\left[\begin{array}{ll} w_1 & w_2 \end{array}\right]=\left[\begin{array}{ll} w_1 \times w_2 & w_1 \times w_2 \\ w_2 \times w_1 & w_2 \times w_2 \end{array}\right]=\left[\begin{array}{cc} w_1^2 & w_1 w_2 \\ w_2 w_1 & w_2^2 \end{array}\right]
  • 取数学期望E（求平均值）：
E[ωωT]=E[[w12w1w2w2w1w22]]=[E[w12]E[w1w2]E[w2w1]E[w22]]E\left[\omega \omega^T\right]=E\left[\left[\begin{array}{cc} w_1^2 & w_1 w_2 \\ w_2 w_1 & w_2^2 \end{array}\right]\right]=\left[\begin{array}{cc} E\left[w_1^2\right] & E\left[w_1 w_2\right] \\ E\left[w_2 w_1\right] & E\left[w_2^2\right] \end{array}\right]

因为噪声均值为0，E(w1)=0E\left(w_1\right)=0，根据方差公式（方差=平方的均值-均值的平方）：

VAR⁡(w1)=E(w12)−[E(w1)]2=E(w12)−0=E(w12)\operatorname{VAR}\left(w_1\right)=E\left(w_1^2\right)-\left[E\left(w_1\right)\right]^2=E\left(w_1^2\right)-0=E\left(w_1^2\right)

另一个角度（μ1\mu_1为0）：

Var⁡(w1)=E[(w1−μ1)2]\operatorname{Var}\left(w_1\right)=E\left[\left(w_1-\mu_1\right)^2\right]

协方差公式：

Cov⁡(w1,w2)=E[(w1−μ1)(w2−μ2)]=E[w1w2]\operatorname{Cov}\left(w_1, w_2\right)=E\left[\left(w_1-\mu_1\right)\left(w_2-\mu_2\right)\right]=E\left[w_1 w_2\right]

噪声均值为0，即μ1\mu_1和μ2\mu_2 为0

Cov⁡(w1,w2)=E[(w1−0)(w2−0)]=E[w1w2]\operatorname{Cov}\left(w_1, w_2\right)=E\left[\left(w_1-0\right)\left(w_2-0\right)\right]=E\left[w_1 w_2\right]

综合

E[wp2]=Var⁡(wp)E[wv2]=Var⁡(wv)E[wpwv]=Cov⁡(wp,wv)\begin{aligned} & E\left[w_p^2\right]=\operatorname{Var}\left(w_p\right) \\ & E\left[w_v^2\right]=\operatorname{Var}\left(w_v\right) \\ & E\left[w_p w_v\right]=\operatorname{Cov}\left(w_p, w_v\right) \end{aligned}

因此，有

Q=E[ωωT]=[Var⁡(wp)Cov⁡(wp,wv)Cov⁡(wv,wp)Var⁡(wv)]Q=E\left[\omega \omega^T\right]=\left[\begin{array}{cc} \operatorname{Var}\left(w_p\right) & \operatorname{Cov}\left(w_p, w_v\right) \\ \operatorname{Cov}\left(w_v, w_p\right) & \operatorname{Var}\left(w_v\right) \end{array}\right]

同理，测量噪声vkv_k满足分布P(v)∼(0,R)P(v) \sim(0, R)，R为协方差矩阵

如何融合

现实中，对于过程噪声ωk−1\omega_{k-1}和测量噪声vkv_k无法建模，我们掌握的只有

x^k−=Ax^k−1+Buk−1zk=Hxk\begin{aligned} & \hat{x}_k^{-}=A \hat{x}_{k-1}+B u_{k-1} \\ & z_k=H x_k \end{aligned}

其中，x^k−\hat{x}_k^{-}是先验估计，即通过状态空间方程去掉过程噪音，计算得到的结果

根据测量结果zkz_k，可以得到

x^kmea =H−zk\hat{x}_{k_{\text {mea }}}=H^{-} z_k

此时，我们有了算出来的结果x^k−\hat{x}_k^{-}和测出来的结果x^kmea \hat{x}_{k_{\text {mea }}}，但噪声依旧是不能被完整建模的

如何通过两个不太准确的结果得到一个准确的结果呢？

使用数据融合：将计算结果和测量结果融合在一起

x^k=x^k−+G(H−zk−x^k−)\hat{x}_k=\hat{x}_k^{-}+G\left(H^{-} z_k-\hat{x}_k^{-}\right)

其中，x^k\hat{x}_k代表后验值

令G=kkHG=k_k H

x^k=x^kˉ+kk(zk−Hx^kˉ)\hat{x}_k=\hat{x}_{\bar{k}}+k_k\left(z_k-H \hat{x}_{\bar{k}}\right)

kk∈[0,H−]k_k \in\left[0, H^{-}\right]，kk=0k_k=0时，x^k−=x^k\hat{x}_k^{-}=\hat{x}_k，选择相信计算结果；Kk=H−K_k=\mathrm{H}^{-}时，x^k=H−zk\hat{x}_k=H^{-} z_k，选择相信计算结果

接下来的目标：寻找KkK_k，使得误差最小，即 x^k→实际值xk\hat{x}_k \rightarrow \text{实际值}x_k

KkK_k与误差有关，比如测量误差大，那么肯定会更愿意相信计算值

引入误差：

ek=xk−x~ke_k=x_k-\tilde{x}_k

eke_k同样满足正态分布 p(lk)∼(0,P)p\left(l_k\right) \sim(0, P)，P为协方差矩阵

P=E[ee⊤]=[σe12σe1σe2σe2σe1σe22]P=E\left[e e^{\top}\right]=\left[\begin{array}{ccc} \sigma e_1^2 & \sigma e_1 \sigma e_2 \\ \sigma e_2 \sigma e_1 & \sigma e_2^2 \end{array}\right]

若估计结果距离实际值越小，则误差的方差也是最小的

那么可以通过一下思路实现这个目标：寻找KkK_k使得P矩阵的迹tr（P）最小

tr⁡(p)=σe12+σe22\operatorname{tr}(p)=\sigma e_1^2+\sigma_{e 2}^2

卡尔曼增益推导过程

下面是实现这一目标的推导过程：

P=E[ee⊤]=E[xk−x^k)(xk−x^k)⊤]\begin{aligned} P & =E\left[e e^{\top}\right] \\ & \left.=E\left[x_k-\hat{x}_k\right)\left(x_k-\hat{x}_k\right)^{\top}\right] \end{aligned}

将x^k=x^kˉ+kk(zk−Hx^kˉ)\hat{x}_k=\hat{x}_{\bar{k}}+k_k\left(z_k-H \hat{x}_{\bar{k}}\right)带入

xk−x^k=xk−(x^kˉ−+kk(zk−Hx^k−))=xk−x^k−−kk(zk)+kkHx^kˉ−=xk−x^k−−kk(Hxk+vk)+kkHx^kˉ−=xk−x^k−−kkHxk−kkvk+kkHx^k−=(xk−x^kˉ)−kkH(xk−x^kˉ)−kkvk=(I−kkH)(xk−x^k−)−kkvk\begin{aligned} x_k-\hat{x}_k & =x_k-\left(\hat{x}_{\bar{k}}^{-}+k_k\left(z_k-H \hat{x}_k^{-}\right)\right) \\ & =x_k-\hat{x}_k^{-}-k_k\left(z_k\right)+k_k H \hat{x}_{\bar{k}}^{-} \\ & =x_k-\hat{x}_k^{-}-k_k\left(H x_k+v_k\right)+k_k H \hat{x}_{\bar{k}}^{-} \\ & =x_k-\hat{x}_k^{-}-k_k H x_k-k_k v_k+k_k H \hat{x}_k^{-} \\ & = \left(x_k-\hat{x}_{\bar{k}}\right)-k_k H\left(x_k-\hat{x}_{\bar{k}}\right)-k_k v_k \\ & =\left(I-k_k H\right)\left(x_k-\hat{x}_k^{-}\right)-k_k v_k \end{aligned}

定义先验误差ek−=xk−x^k−e_k^{-}=x_k-\hat{x}_k^{-}，则

P=E[ee⊤]=E[xk−x^k)(xk−x^k)⊤]=E[((I−kkH)ek−−kkvk][(I−kkH)ek−−kkVk)]⊤]\begin{aligned} P & =E\left[e e^{\top}\right] \\ & \left.=E\left[x_k-\hat{x}_k\right)\left(x_k-\hat{x}_k\right)^{\top}\right] \\ & =\left.E\left[\left(\left(I-k_k H\right) e_k^{-}-k_k v_k\right]\left[\left(I-k_k H\right) e_k^{-}-k_k V_k\right)\right]^{\top}\right] \end{aligned}

由(AB)⊤=B⊤A⊤(A+B)⊤=A⊤+B⊤\begin{gathered}(A B)^{\top}=B^{\top} A^{\top} \\ (A+B)^{\top}=A^{\top}+B^{\top}\end{gathered}，所以先写出第二项的转置：

[(I−kkH)ek−−kkvk)]⊤=ek−⊤(I−kkH)⊤−vk⊤kk⊤\left.\left[\left(I-k_k H\right) e_k^{-}-k_k v_k\right)\right]^{\top}=e_k^{-\top}\left(I-k_k H\right)^{\top}-v_k^{\top} k_k^{\top}

展开括号内的乘积，原式等于

P=E[(I−kkH)ek−ek−⊤(I−kkH)⊤−(I−kkH)ek−vk⊤kk⊤−kkvkek−⊤(I−kkH)⊤+kkvkvk⊤kk⊤]P=E\left[\left(I-k_k H\right) e_k^{-} e_k^{-\top}\left(I-k_k H\right)^{\top}-\left(I-k_k H\right) e_k^{-} v_k^{\top} k_k^{\top}-k_k v_k e_k^{-\top}\left(I-k_k H\right)^{\top}+k_k v_k v_k^{\top} k_k^{\top}\right]

对其中的每一项单独求期望：

提出常数

E[(I−kkH)ek−vk⊤kk⊤]=(I−kkH)E[ek−vk⊤]kk⊤=0E\left[\left(I-k_k H\right) e_k^{-} v_k^{\top} k_k^{\top}\right]=\left(I-k_k H\right) E\left[e_k^{-} v_k^{\top}\right] k_k^{\top}=0

若A、B相互独立，则有E(AB)=E(A)E(B)E(A B)=E(A) E(B)，由于ek−{e_k}^{-}与v_k不相关且各自的均值为零，因此交叉项期望为零

同理：

E[kkvkek−⊤(I−kkH)⊤]=0E\left[k_k v_k e_k^{-\top}\left(I-k_k H\right)^{\top}\right]=0

于是

P=(I−kkH)E[ek−ek−⊤](I−kkH)⊤+kkE[vkvk⊤]kk⊤P=\left(I-k_k H\right) E\left[e_k^{-} e_k^{-\top}\right]\left(I-k_k H\right)^{\top}+k_k E\left[v_k v_k^{\top}\right] k_k^{\top}

由协方差矩阵形式P(v)∼(0,R)P(v) \sim(0, R)，E[vv⊤]=RE\left[v v^{\top}\right]=R，记Pk−=E[ek−ek−⊤],Rk=E[vkvk⊤]P_k^{-}=E\left[e_k^{-} e_k^{-\top}\right], \quad R_k=E\left[v_k v_k^{\top}\right]

Pk=(I−kkH)Pk−(I−kkH)⊤+kkRkkk⊤=(Pk−−kkHPk−)(I⊤−H⊤kk⊤)+kkRkk⊤=Pk−−kkHPk−−Pk−H⊤kk⊤+kkHPk−H⊤kk⊤+kkRkk⊤\begin{aligned} P_k & =\left(I-k_k H\right) P_k^{-}\left(I-k_k H\right)^{\top}+k_k R_k k_k^{\top} \\ & =\left(P_k^{-}-k_k H P_k^{-}\right)\left(I^{\top}- H^{\top}k_k^{\top}\right)+k_k R k_k^{\top} \\ & =P_k^{-}-k_k H P_k^{-}-P_k^{-} H^{\top} k_k^{\top}+k_k H P_k^{-} H^{\top} k_k^{\top}+k_k R k_k^{\top} \end{aligned}

这就是误差的协方差矩阵合并后的表达式，通常用于卡尔曼滤波中推导最优增益kkk_k时对PkP_k的展开

还记得目标是什么吗？目标是估计和实际的误差最小，通过P矩阵的迹反映

tr⁡(Pk)=tr⁡(Pk−)−2tr⁡(kkHPk−)+tr⁡(kkHPk−H⊤kk⊤)+tr⁡(kkRkk⊤)\begin{aligned} \operatorname{tr}\left(P_k\right)=\operatorname{tr}\left(P_k^{-}\right)-2 \operatorname{tr}\left(k_k H P_k^{-}\right) & +\operatorname{tr}\left(k_k H P_k^- H^{\top} k_k^{\top}\right) +\operatorname{tr}\left(k_k R k_k^{\top}\right) \end{aligned}

通过dtr⁡(pk)dkk=0\frac{d \operatorname{tr}\left(p_k\right)}{d k_k}=0来寻找使迹最小的kkk_k

结合一些计算公式，最终可以得到

Kk=Pk−H⊤HPk−H⊤+RK_k=\frac{P_k^{-} H^{\top}}{H P_k^{-} H^{\top}+R}

当测量噪声协方差矩阵R很大时，kk→0k_k \rightarrow 0

x^k=x^k−\hat{x}_k=\hat{x}_k^{-}

取先验估计作为估计值

卡尔曼滤波数据融合流程

对于系统：

Xk=AXk−1+BUk−1+Wk−1ω∼p(0,Q)Zk=HXk+vkv∼p(0,R)\begin{array}{ll} X_k=A X_{k-1}+B U_{k-1}+W_{k-1} & \omega \sim p(0, Q) \\ Z_k=H X_k+v_k & v \sim p (0, R) \end{array}

我们有：

先验估计：

x^k−=Ax^k−1+Buk−1\hat{x}_k^{-}=A \hat{x}_{k-1}+B u_{k-1}

后验估计，使用了数据融合，选取不同的kkk_k，就会不同程度倾向于观测或者计算结果：

x^k=x^k−+kk(zk−Hx^k−)\hat{x}_k=\hat{x}_k^{-}+k_k\left(z_k-H \hat{x}_k^{-}\right)

卡尔曼增益：

kR=Pk−H⊤HPk−H⊤+Rk_R=\frac{P_k^{-} H^{\top}}{H P_k^{-} H^{\top}+R}

对于以上的公式，我们缺少的是Pk−P_k^{-}的信息，因此需要求出Pk−P_k^{-}

Pk−=E[ek−ek−T]P_k^{-}=E\left[e_k^{-} e_k^{-T}\right]

先验误差为真实值减去先验估计值

ek−=xk−x^k−=Axk−1+Buk−1+ωk−1−Ax^k−1−Buk−1=A(xk−1−x^k−1)+wk−1=Aek−1+ωk−1\begin{aligned} e_k^{-}= & x_k-\hat{x}_k^{-} \\ & = A x_{k-1}+B u_{k-1}+\omega_{k-1}-A \hat{x}_{k-1}-B u_{k-1} \\ & =A\left(x_{k-1}-\hat{x}_{k-1}\right)+w_{k-1} \\ & =A e_{k-1}+\omega_{k-1} \end{aligned}
Pk−=E[ek−ek−T]=E[(Aek−1+ωk−1)(Aek−1+ωk−1)⊤]=E[(Aek−1+ωk−1)(ek−1⊤A⊤+ωk−1⊤)]=E[Aek−1ek−1⊤A⊤+Aek−1ωk−1⊤+ωk−1ek−1⊤A⊤+ωk−1ωk−1⊤]\begin{aligned} P_k^{-}& =E\left[e_k^{-} e_k^{-T}\right] \\ & = E\left[\left(A e_{k-1}+\omega_{k-1}\right)\left(A e_{k-1}+\omega_{k-1}\right)^{\top}\right] \\ & =E\left[\left(A e_{k-1}+\omega_{k-1}\right)\left(e_{k-1}^{\top} A^{\top}+\omega_{k-1}^{\top}\right)\right] \\ & =E\left[A e_{k-1} e_{k-1}^{\top} A^{\top}+A e_{k-1} \omega_{k-1}^{\top}+\omega_{k-1} e_{k-1}^{\top} A^{\top}+\omega_{k-1} \omega_{k-1}^{\top}\right] \end{aligned}

对其中的项分别求期望，E(ek−1wk−1)=E(ek−1)E(wk−1)E(e_{k-1}w_{k-1})=E(e_{k-1})E(w_{k-1})，E(ek−1)=0,E(wk−1)=0E(e_{k-1})=0,E(w_{k-1})=0

所以原式

=AE[ek−1ek−1⊤]A⊤+E[wk−1wk−1⊤]=APk−1A⊤+Q\begin{aligned} & =A E\left[e_{k-1} e_{k-1}^{\top}\right] A^{\top}+E\left[w_{k-1} w_{k-1}^{\top}\right] \\ & =A P_{k-1} A^{\top}+Q \\ \end{aligned}

现在我们就有了先验误差的协方差矩阵表示了，可以利用卡尔曼滤波器估计状态变量的值了

分为两个步骤：预测和校正

image.png

有了这五步，就可以得到卡尔曼滤波的最优估计值了

扩展卡尔曼滤波

系统表达

xk=f(xk−1,μk−1,wk−1)zk=h(xk,vk)\begin{aligned} & x_k=f\left(x_{k-1}, \mu_{k-1}, w_{k-1}\right) \\ &z_k=h\left(x_k, v_k\right) \end{aligned}

其中，f 和 h为非线性函数；w 和 v 为过程噪声与观测噪声

状态方程的泰勒展开

问题：当一个正态分布（高斯分布）的随机变量通过非线性系统（f或 h）后，其分布将不再保持正态性。这使得基于高斯假设的经典卡尔曼滤波器无法直接应用

解决方案：为了处理非线性，引入线性化技术，核心工具是泰勒展开

选取展开点：

  • 对于状态方程：在滤波过程中，系统的真实状态xkx_k是未知的（存在误差），因此无法在真实点进行线性化，因此选择在上一次的最优估计点x^k−1x̂_{k-1}（即后验估计）作为泰勒展开的参考点
  • 通常将过程噪声wk−1w_{k-1}在其均值点（0点）附近进行线性化
  • uk−1u_{k-1}是已知的确定性输入，而非待估计的随机变量，因此uk−1u_{k-1}是作为展开点的一个已知坐标代入的
xk=f(xk−1,uk−1,wk−1)≈f(x^k−1,uk−1,0)+∂f∂x∣(x^k−1,0)⋅(xk−1−x^k−1)+∂f∂w∣(x^k−1,0)⋅(wk−1−0)\begin{aligned} x_k & =f\left(x_{k-1}, u_{k-1}, w_{k-1}\right) \\ & \approx f\left(\hat{x}_{k-1}, u_{k-1}, 0\right)+\left.\frac{\partial f}{\partial x}\right|_{\left(\hat{x}_{k-1}, 0\right)} \cdot\left(x_{k-1}-\hat{x}_{k-1}\right)+\left.\frac{\partial f}{\partial w}\right|_{\left(\hat{x}_{k-1}, 0\right)} \cdot\left(w_{k-1}-0\right) \end{aligned}

将非线性函数 f 在点 (x^k−1\hat{x}_{k-1}, 0)处，围绕其两个变量xk−1 x_{k-1}和wk−1 w_{k-1}展开，偏导都是对第一个和第三个自变量求的，因为第二个自变量控制输入 uk−1u_{k-1}是已知的，不参与线性化

定义状态方程的雅可比矩阵

  • 状态雅可比矩阵Ak−1A_{k-1}：
Ak−1=∂f∂x∣(x^k−1,uk−1,0)A_{k-1}=\left.\frac{\partial f}{\partial x}\right|_{\left(\hat{x}_{k-1}, u_{k-1}, 0\right)}
  • 过程噪声雅可比矩阵Wk−1W_{k-1}:
Wk−1=∂f∂w∣(x^k−1,uk−1,0)W_{k-1}=\left.\frac{\partial f}{\partial w}\right|_{\left(\hat{x}_{k-1}, u_{k-1}, 0\right)}

代入后，线性化方程变为：

xk≈f(x^k−1,uk−1,0)+Ak−1(xk−1−x^k−1)+Wk−1wk−1x_k \approx f\left(\hat{x}_{k-1}, u_{k-1}, 0\right)+A_{k-1}\left(x_{k-1}-\hat{x}_{k-1}\right) +W_{k-1} w_{k-1}

观测方程的泰勒展开

选取展开点：

  • 对于观测方程：在 k 时刻，我们尚未得到测量值 zkz_k之前，我们拥有的是基于 k-1时刻信息的状态预测值xk−x_k^-, xk−=f(x^k−1,uk−1,0)x_k^- = f(x̂ₖ₋₁, uₖ₋₁, 0)
  • 计算 k 时刻状态的先验状态估计xk−x_k^-
  • 噪声在其均值点线性化：通常假设测量噪声 vkv_k的均值为0，所以我们在线性化时，将vkv_k设为其均值 0

因此，标准EKF的线性化点为：(xk−x_k^-, 0)

zk=h(xk,vk)≈h(xk−,0)+∂h∂x∣(xk−,0)⋅(xk−xk−)+∂h∂v∣(xk−,0)⋅(vk−0)\begin{aligned} z_k & =h\left(x_k, v_k\right) \\ & \approx h\left(x_k^-, 0\right)+\left.\frac{\partial h}{\partial x}\right|_{\left(x_k^-, 0\right)} \cdot\left(x_k-x_k^-\right)+\left.\frac{\partial h}{\partial v}\right|_{\left(x_k^-, 0\right)} \cdot\left(v_k-0\right) \end{aligned}

定义观测方程的雅可比矩阵

  • 测量雅可比矩阵HkH_k
Hk=∂h∂x∣(xk−,0)H_k=\left.\frac{\partial h}{\partial x}\right|_{\left(x_k^-, 0\right)}
  • 测量噪声雅可比矩阵VkV_k
Vk=∂h∂v∣(xk−,0)V_k=\left.\frac{\partial h}{\partial v}\right|_{\left(x_k^-, 0\right)}

代入后，方程变为：

zk≈h(xk−,0)+Hk(xk−xk−)+Vkvkz_k \approx h\left(x_k^-, 0\right)+H_k \left(x_k-x_k^-\right)+V_k v_k

扩展卡尔曼滤波的标准更新方程

xk−=f(x^k−1,Uk−1,0)Pk−=APk−1AT+WQWTKk=(Pk−HT)/(HPk−HT+VRVT)x^k=xk−+Kk(zk−h(xk−,0))Pk=(I−KkH)Pk−\begin{aligned} & xₖ⁻ = f(x̂ₖ₋₁, Uₖ₋₁, 0) \\ & Pₖ⁻ = A Pₖ₋₁ Aᵀ + W Q Wᵀ \\ & Kₖ = (Pₖ⁻ Hᵀ) / (H Pₖ⁻ Hᵀ + V R Vᵀ) \\ & x̂ₖ = xₖ⁻ + Kₖ (zₖ - h(xₖ⁻, 0)) \\ & Pₖ = (I - Kₖ H) Pₖ⁻ \end{aligned}

本文作者:cc

本文链接:

版权声明:本博客所有文章除特别声明外，均采用 BY-NC-SA 许可协议。转载请注明出处！