论文阅读:
- 风机叶片无人机自主巡检系统控制算法研究
- 风机叶片的无人机自主巡检系统
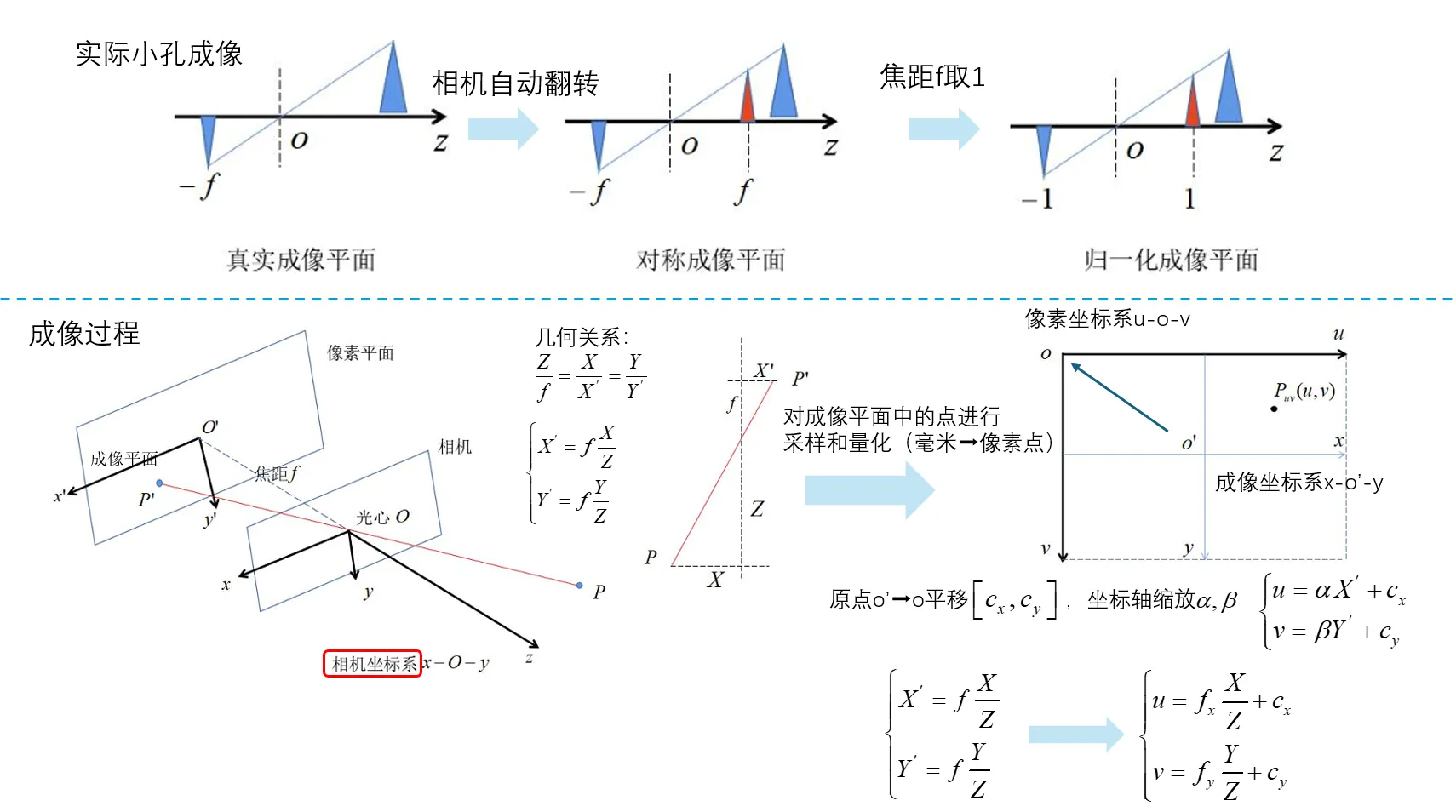
将αf记为fx,表示将βf记为fy,有:
{u=fxZX+cxv=fyZY+cy
以上公式写成矩阵形式有:
uv1=Z1fx000fy0cxcy1XYZ=Z1KP
将Z消除归一化为
uv1=fx000fy0cxcy1X/ZY/Z1=KX1′Y1′1=KP1′
其中K为相机的内参矩阵,在相机出厂的时候就已经确定的固定参数,有些相机说明上会有K矩阵的详细参数,而有些则需要自己计算,计算的方法就涉及到相机的标定。
相机成像中坐标变换——
坐标系旋转
二维
三维坐标投影至X-O-Y平面,Z轴朝外,X-O-Y坐标轴绕Z轴逆时针旋转θ角度得到X'-O'-Y'坐标系,P(X, Y, Z)变为P′(X′,Y′,Z′)
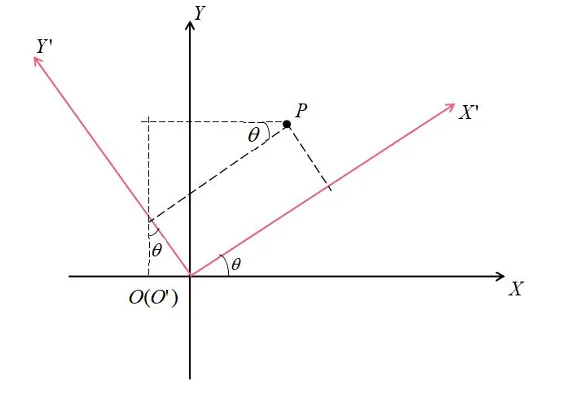
由几何关系:
{X=X′⋅cosθ−Y′⋅sinθY=X′⋅cosθ+Y′cosθ
转换为矩阵:
[X′Y′]=[cosθ−sinθsinθcosθ][XY]=r[XY][XY]=[cosθsinθ−sinθcosθ][X′Y′]=r′[X′Y′]
三维
同理,根据二维坐标的旋转可以推导出三维坐标系轴旋转的旋转矩阵表达形式。三维坐标系的轴旋转可以先将一个坐标轴固定从而转化为二维坐标系旋转,再分别对X、Y、
Z轴依次操作可得:
X′Y′Z′=1000cosθ−sinθ0sinθcosθXYZ=RXXYZX′Y′Z′=cosθ0sinθ010−sinθ0cosθXYZ=RYXYZX′Y′Z′=cosθ−sinθ0sinθcosθ0001XYZ=RZXYZ
其中RX、RY、RZ分别表示绕X、Y、Z轴旋转的三维旋转矩阵,若按照Z→Y→Z的顺序旋转,得到整体旋转矩阵R=RXRYRZ
相机坐标系和世界坐标系可以通过旋转矩阵Rcn(把“相机坐标中的向量”表达到“世界坐标”中的旋转)联系起来:
- 世界←相机:Pn=RcnPc+T
- 世界→相机:Pc=Rnc(Pn−T)
Pn=[xn,yn,zn]T表示世界坐标系下的坐标,Pc=[xc,yc,zc]T表示相机坐标系下的坐标,T表示平移
投影:相机坐标 → 归一化成像平面
小孔成像模型,焦距为 f
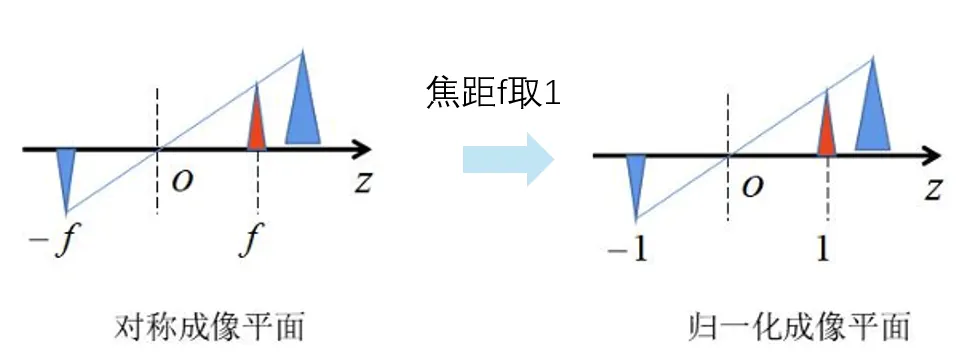
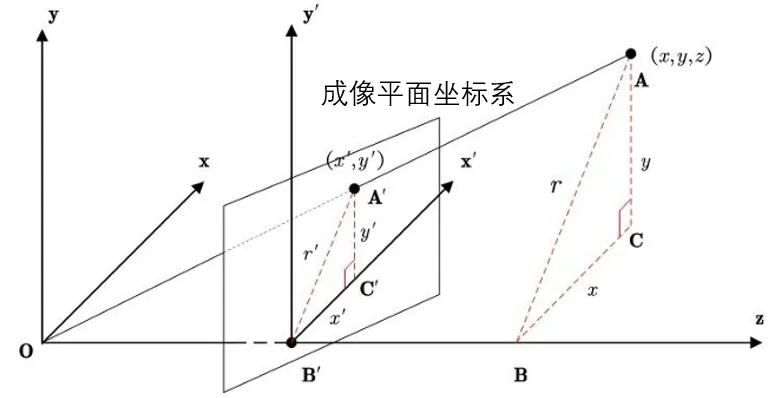 xd=fzcxc,yd=fzcyc
xd=fzcxc,yd=fzcyc
用齐次形式:
xdyd1=zc1⋅f000f0001000xcyczc1
相机坐标Pc=[xc,yc,zc]T→归一化的成像平面坐标Pd=[xd,yd,1]T
成像平面坐标 → 像素坐标
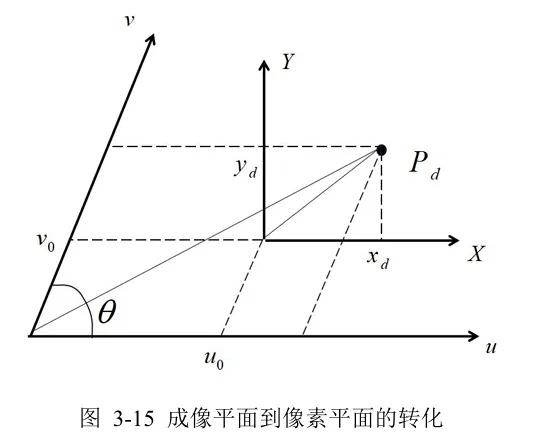
- 用主点坐标 (u0,v0) 把原点从主点移动到像素系原点
- dxxd、dyyd表示像素增量
dx, dy:单个像素的物理尺寸(米/像素),其倒数把米换成像素:例如,
- 传感器像素间距:dx, dy(例如 4 μm/像素)
- 成像平面坐标 xd,yd 的单位是米/毫米
- 像素数 = 物理长度 ÷ 像素间距,所以 x 像素增量是 x_d/dx,y 像素增量是 y_d/dy。
取α=dx1,β=dy1,写成齐次坐标的形式可得:
uv1=α000β0u0v01xdyd1
归一化的成像平面坐标Pd=[xd,yd,1]T→像素平面坐标(u,v)
xd=fzcxc,yd=fzcyc
uv1=αf000βf0u0v01xdyd1
fx=af,fy=βf
相机坐标系下的坐标→像素平面坐标:
uv1=Kfx000fy0u0v01xc/zcyc/zc1
uv1=zc1KxcyczcK=fx000fy0u0v01
结合
以上步骤结合起来,即:
ZCuv1=dx1000dy10u0v01f000f0001000[R01×3t1]XWYWZW1
XWYWZW1为世界坐标系的点,u、v为像素坐标系下坐标
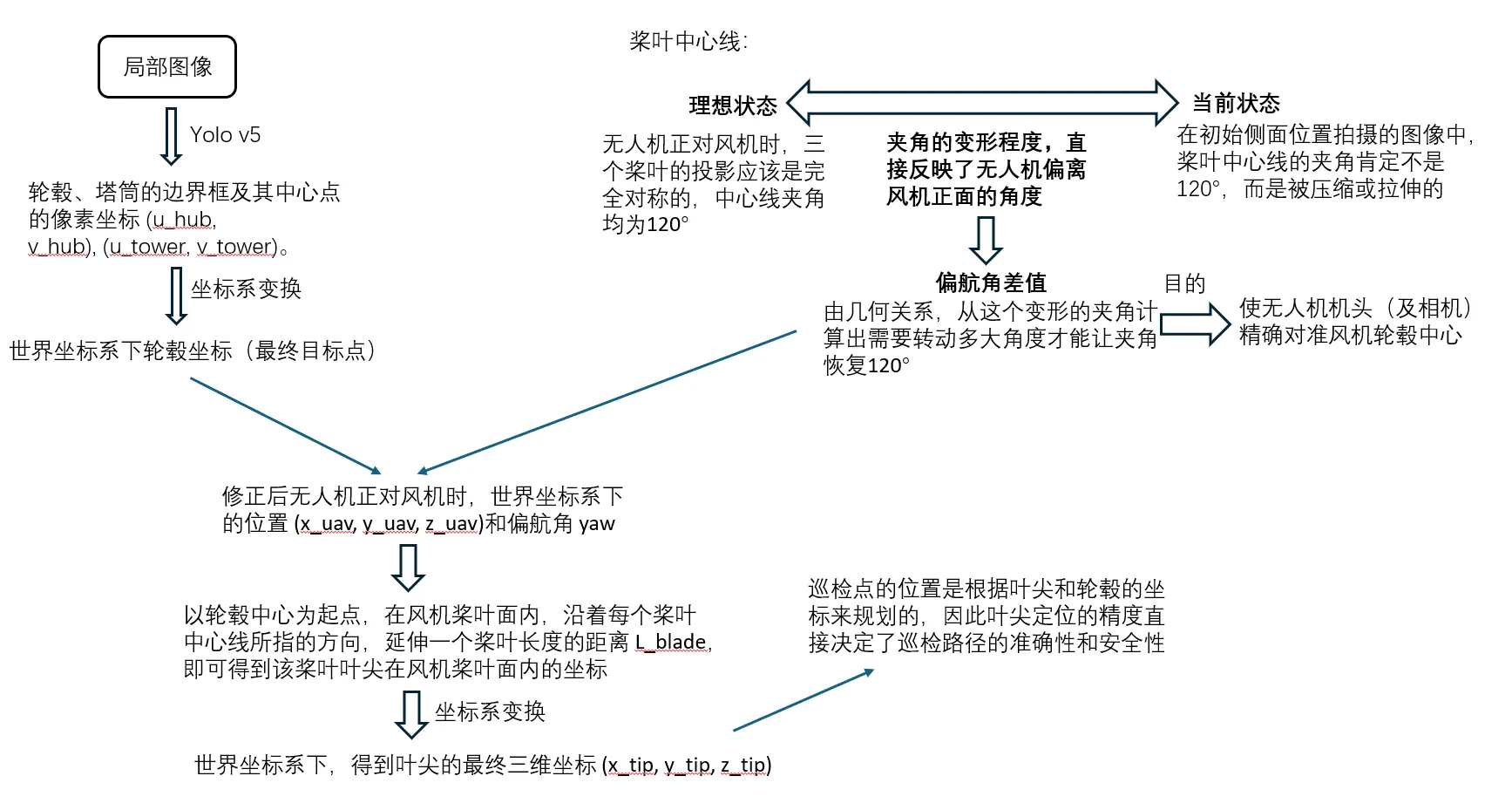
论文《无人机自主巡检系统/风机叶片无人机自主巡检系统控制算法研究》第三章思路
如何“正对”